- 社交网络与文本分析课程
8 网络嵌入式表示及应用
刘跃文 教授、博导西安交通大学 管理学院
联系方式: liuyuewen@xjtu.edu.cn2023年4月16日 版本1.2
提纲¶
- 万物皆可embedding
- DeepWalk
- Node2Vec
Jure的图深度学习课: http://web.stanford.edu/class/cs224w/index.html#content
1. 万物皆可embedding¶
1.1 重新思考embedding¶
- embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义。
- 比如 Embedding(复仇者联盟)和Embedding(钢铁侠)之间的距离就会很接近,但 Embedding(复仇者联盟)和Embedding(乱世佳人)的距离就会远一些。
除此之外Embedding甚至还具有数学运算的关系,比如 Embedding(马德里)-Embedding(西班牙)+Embedding(法国)≈Embedding(巴黎)
从另外一个空间表达物体,甚至揭示了物体间的潜在关系,从某种意义上来说,Embedding方法甚至具备了一些本体论的哲学意义。
- Embedding能够用低维向量对物体进行编码还能保留其含义的特点非常适合深度学习。
- 传统机器学习模型构建过程中经常使用one hot encoding对离散特征,特别是id类特征进行编码,但由于one hot encoding的维度等于物体的总数,比如阿里的商品one hot encoding的维度就至少是千万量级的。这样的编码方式对于商品来说是极端稀疏的.
- 甚至用multi hot encoding对用户浏览历史的编码也会是一个非常稀疏的向量。
- 而深度学习的特点以及工程方面的原因使其不利于稀疏特征向量的处理,如果能把物体编码为一个低维稠密向量再喂给DNN,是一个高效的基本操作。
1.2 从word2vec到item2vec¶
在word2vec诞生之后,embedding的思想迅速从NLP领域扩散到几乎所有机器学习的领域,既然可以对一个序列中的词进行embedding,那自然可以对用户购买序列中的一个商品,用户观看序列中的一个电影进行embedding。而广告、推荐、搜索等领域用户数据的稀疏性几乎必然要求在构建DNN之前对user和item进行embedding后才能进行有效的训练。
具体来讲,如果item存在于一个序列中,item2vec的方法与word2vec没有任何区别。而如果我们摒弃序列中item的空间关系,在原来的目标函数基础上,自然是不存在时间窗口的概念了,取而代之的是item set中两两之间的条件概率。
2. DeepWalk (2014年)¶
2.1 DeepWalk 简介¶
- Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2014: 701-710. Download
- 这篇论文主要提出了在一个网络中,学习节点隐表达的方法——DeepWalk,这个方法在一个连续向量空间中对节点的社会关系进行编码,是语言模型和无监督学习从单词序列到图上的一个扩展。该方法将截断游走的序列当成句子进行学习。该方法具有可扩展,可并行化的特点,可以用来做网络分类和异常点检测。
- 论文贡献有三点:
- 将深度学习应用到图分析中,构建鲁棒性的表示,其结果可应用于统计模型中
- 将表示结果应用于一些社会网络的多标签分类任务中,与对比算法比较,大部分的$F_1$值提高$5-10%$,有些情况下,在给定少于60%训练集的情况下,比其他对比方法要好;
- 论文通过构建互联网规模(例如YouTube)的并行化实现的表示,论证了方法的可扩展性,同时描述了构建流式版本的方法实现
资料来源:https://blog.csdn.net/osuperman12345/article/details/65444832
- DeepWalk原理简介
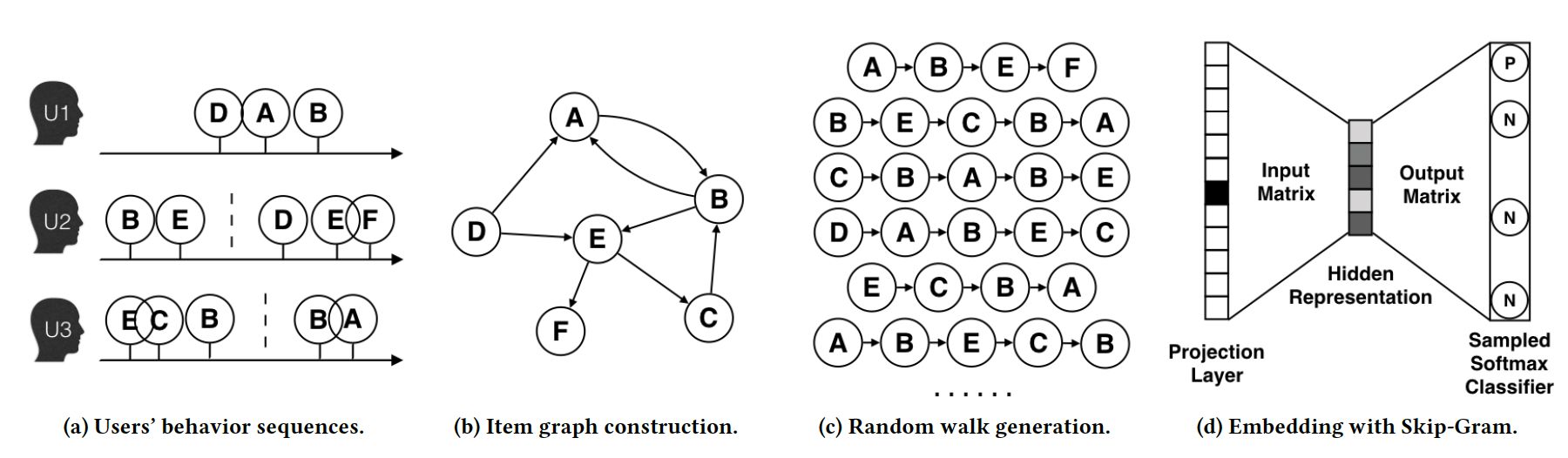
图来源:Jizhe Wang, Pipei Huang, Huan Zhao, Zhibo Zhang, Binqiang Zhao, Dik Lun Lee. "Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba." SIGKDD explorations Udisk (2018). Download
2.2 DeepWalk的论文解读¶
给定一个图$G=(V,E)$,以及部分标注的社会网络$G_L=(V,E,X,Y)$,其中,$X\in \mathbb{R}^{|V|\times S}$是节点属性,$S$是每个属性向量的特征空间的大小,$Y\in \mathbb{R}^{|V|\times |y|}$是节点的标签。论文的工作就是独立于标签$Y$的值,学习出$X_E \in \mathbb{R}^{|V|\times d}$的表示,$d$是一个极小的隐空间维度。学习出来的社会化表示具有以下特点:
- 自适应性,真实的社会网络是不断变化的,新的社会化关系进来之后,不需要再重新执行一次学习过程
- 社区感知性,学出来的隐空间应该能够包含网络中同质节点或相似节点距离近的信息
- 低维度
- 连续性
选取随机游走序列,作为DeepWalk的输入。原因有:
- 随机游走能够包含网络的局部结构
- 使用随机游走可以很方便地并行化
- 当网络结构具有微小的变化时,可以针对变化的部分生成新的随机游走,更新学习模型,提高了学习效率
- 如果一个网络的节点服从幂律分布,那么节点在随机游走序列中的出现次数也应该服从幂律分布,论文通过实证发现自然语言处理中单词的出现频率也服从幂律分布。可以很自然地将自然语言处理的相关方法直接用于构建社区结构模型中。
- 针对一个自然语言处理问题,给定一个单词序列$W^{n}_{1}=(w_0,w_1,...,w_n)$,我们要用前$n-1$个单词来预测第$n$个单词,也就是最大化$Pr(w_n|w_0,w_1,...,w_{n-1})$的问题。针对社会网络上的随机游走序列,我们自然会想到,要用前$n-1$个节点来预测第$n$个节点的出现$Pr(v_n|v_0,v_1,...,v_{n-1})$。但是论文的目的是要学习一个隐表示,所以引入了一个映射函数$\Phi : v\in V \mapsto \mathbb{R}^{|V|\times d}$。于是,问题变成估计$Pr(v_n|\Phi(v_0),\Phi(v_1),...,\Phi(v_{n-1}))$的问题。但是如果随机游走的长度变大,会降低该条件概率估计的效率。
- 自然语言处理领域中,针对这个问题给出了几个解决方案:
- 把根据上下文预测一个单词的问题,变为根据一个单词预测上下文的问题
- 在一个给定单词的左边和右边都会出现上下文内容
- 去除单词出现的顺序约束
于是问题变成了最优化如下式子 $minimize_\Phi −logPr(\{v_{i−w},...,v_{i+w}\}\setminus v_i|\phi(v_i))$
这里$\setminus v_i$是去除、不包括$v_i$的意思。
- 算法包含两个主要部分:一个随机游走生成器和一个更新过程。
- 随机游走生成器随机均匀地选取网络节点,并生成固定长度的随机游走序列,每个节点生成长度为$t$的$\gamma$个随机游走序列,本文并没有使用重启的随机游走方法。为了加快算法的收敛,本文对图中所有的节点遍历一遍之后,再重新遍历所有节点,论文使用SkipGram算法来更新节点表示。SkipGram首先将每个节点$v_i$与其表示一一映射,并有假设:$Pr(\{v_{i-w},...,v_{i+w}\}\setminus v_i | \Phi(v_i))=\prod^{i+w}_{j=i-w,j\ne i} Pr(v_j|\Phi (v_i))$,通过最大化这个概率,来更新$\Phi$的值。
- 因为使用逻辑回归的方法,太耗时了,本文使用分层softmax的方法来训练。即将每个节点分配到二分类树的叶子节点上,本文使用哈夫曼编码对节点进行编码,将出现频繁的节点的路径设置较短。假设从根节点到一个节点$u_k$的路径是一个树节点的序列$(b_0,b_1,...,b_{[log|V|]})$,$b_0$是根节点,$b_{[log|V|]}$表示节点$u_k$,于是有$Pr(u_k|\Phi(v_j))=\prod^{[log|V|]}_{l=1}Pr(b_l |\Phi (v_j))$,其中,$Pr(b_l |\Phi (v_j))=1/(1+e^{-\Phi(v_j)*\Psi(b_l)})$,$\Psi(b\_l)$是树上节点$b_l$的父亲节点的隐表示。例如,在下图中,从根节点到$v_3$节点的路径应为$b1,b2,b5,v3$将这些节点对应的概率累积算出来。
- DeepWalk论文中插图
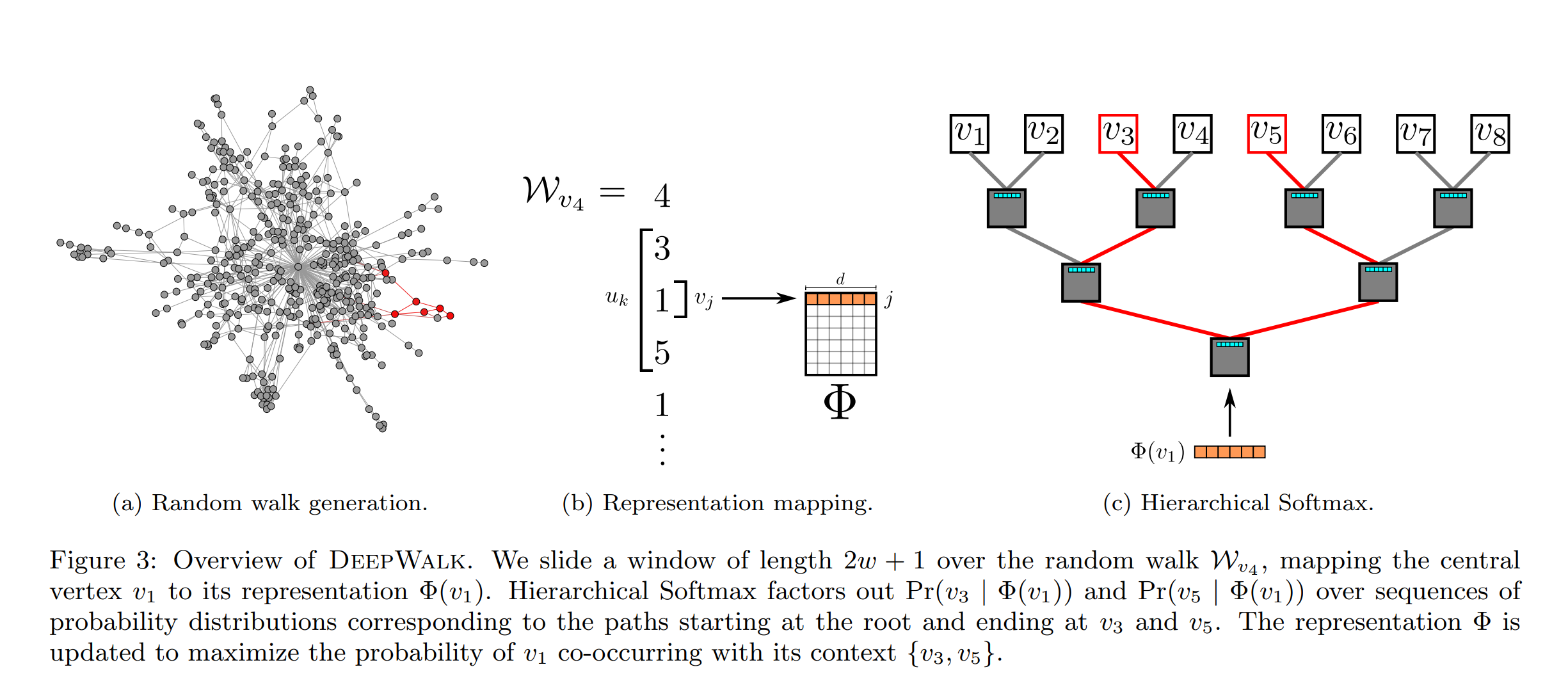
- DeepWalk的算法

#pip install deepwalk
#pip install python-Levenshtein
from gensim.models import Word2Vec
import networkx as nx
# 定义随机游走策略
from deepwalk import DeepWalk
# 加载网络数据
G = nx.read_adjlist('karate.adjlist')
deepwalk = DeepWalk(G, num_walks=10, walk_length=80, window=5, workers=4)
# 训练模型
model = deepwalk.fit(window=5, min_count=1)
# 获取节点嵌入向量
embedding = model.wv.vectors
# 检索与相似度最高的节点对
similarity_matrix = np.dot(embedding, np.transpose(embedding))
non_edges = list(nx.non_edges(G))
scores = []
for (i, j) in non_edges:
scores.append((i, j, similarity_matrix[i][j]))
# 按相似度分数从高到低排序
scores = sorted(scores, key=lambda x: x[-1], reverse=True)
# 输出前10个预测的新链接和相似度分数
print("Top 10 predicted new links:")
for i, (u, v, score) in enumerate(scores[:10]):
print(f"{i + 1}. ({u}, {v}) - {score}")
2.3.2 deepwalk的另一种实现¶
## Deepwalk
import numpy as np
import random
from tqdm import tqdm
import warnings
warnings.filterwarnings('ignore')
from sklearn.decomposition import PCA
import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd
from gensim.models import Word2Vec
%matplotlib inline
df_data = pd.read_csv("./data/space_data.tsv", sep = "\t")
df_data.head()
g = nx.from_pandas_edgelist(df_data, "source", "target", edge_attr=True, create_using=nx.Graph())
def get_random_walk(node, pathlength):
random_walk = [node]
for i in range(pathlength-1):
tmp = list(g.neighbors(node))
tmp = list(set(tmp) - set(random_walk))
if len(tmp) == 0:
break
ran_node = random.choice(tmp)
random_walk.append(ran_node)
node = ran_node
return random_walk
allnodes = list(g.nodes())
walks_list_random = []
for n in tqdm(allnodes):
for i in range(5):
walks_list_random.append(get_random_walk(n,10))
# count of sequences
len(walks_list_random)
model = Word2Vec(window = 4, sg = 1, hs = 0,
negative = 9,
alpha=0.04, min_alpha=0.0005,seed = 20)
model.build_vocab(walks_list_random, progress_per=2)
model.train(walks_list_random, total_examples = model.corpus_count, epochs=20, report_delay=1)
model.wv.most_similar('artificial intelligence',topn=10)
3. Node2Vec(2016年)¶
3.1 Node2Vec 介绍¶
- Aditya Grover and Jure Leskovec. 2016. Node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '16). Association for Computing Machinery, New York, NY, USA, 855–864. https://doi.org/10.1145/2939672.2939754 Download
- Node2Vec的思想跟DeepWalk类似,不过改进了DeepWalk中随机游走的生成方式,使得生成的随机游走可以反映深度优先和广度优先两种采样的特性,从而增加单词嵌入的准确性,提高网络嵌入的效果。
- 论文下载
- 相比于Deepwalk 中图的随机游走策略,Node2Vec通过调整随机游走的概率,使得graph embedding的结果在“同质性”和“结构性”中进行权衡。
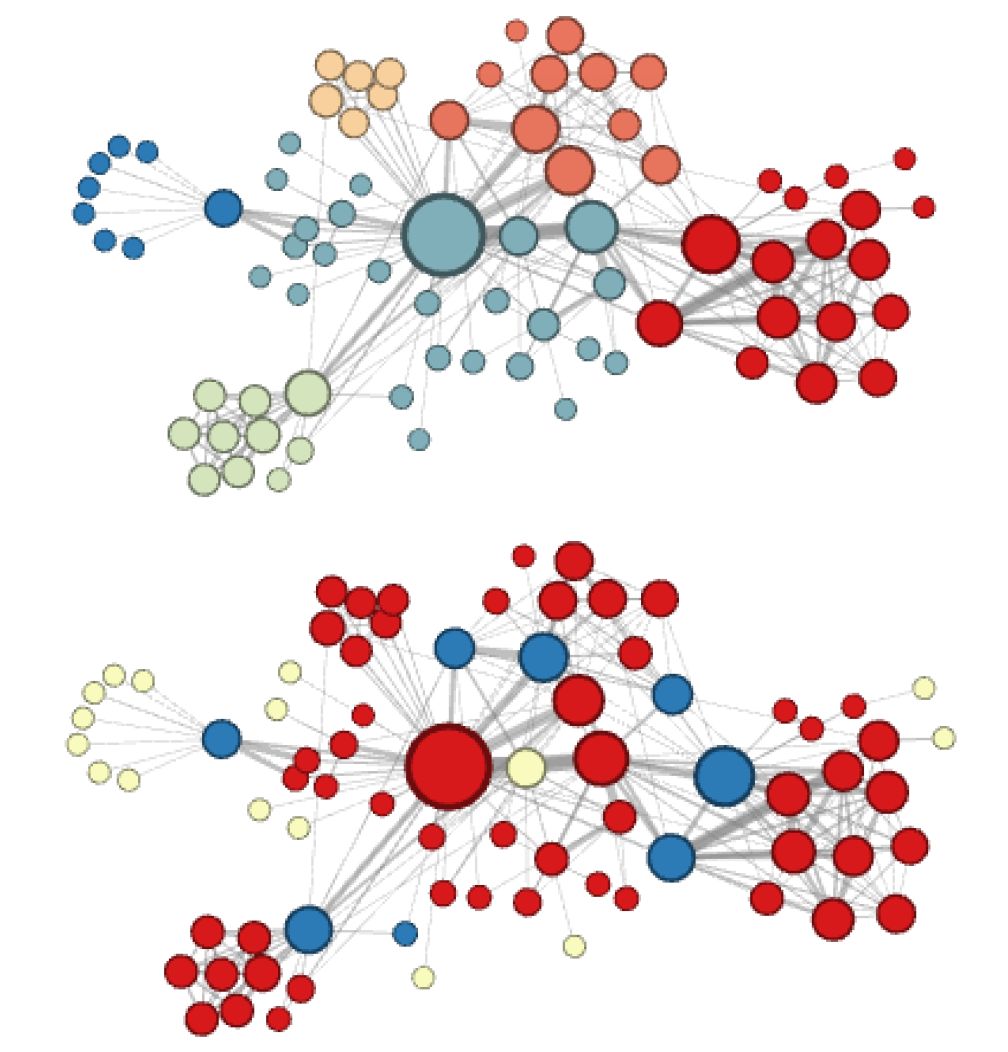
- 如下图:其中“同质性”指的是相邻的网络节点中,embedding表达应该相似,例如
u与s1节点。而“结构性”指的是结构相似的网络节点中需要具有相似的embedding表达,例如u与s6节点。为了表达图网络的结构性,我们应该采用「BFS」 (Breadth First Search,宽度优先搜索) 的方法来进行采样。这是因为BFS可以扫描局部的结构。同时为了表达图结构的同质性,我们采用「DFS」 (Depth First Search,深度优先搜索) 的方法来进行扫描。通过调整随机游走的概率,其扫描过程可以在BFS和DFS之间进行权衡,我们下面将详细讲述。
- BFS和DFS的算法
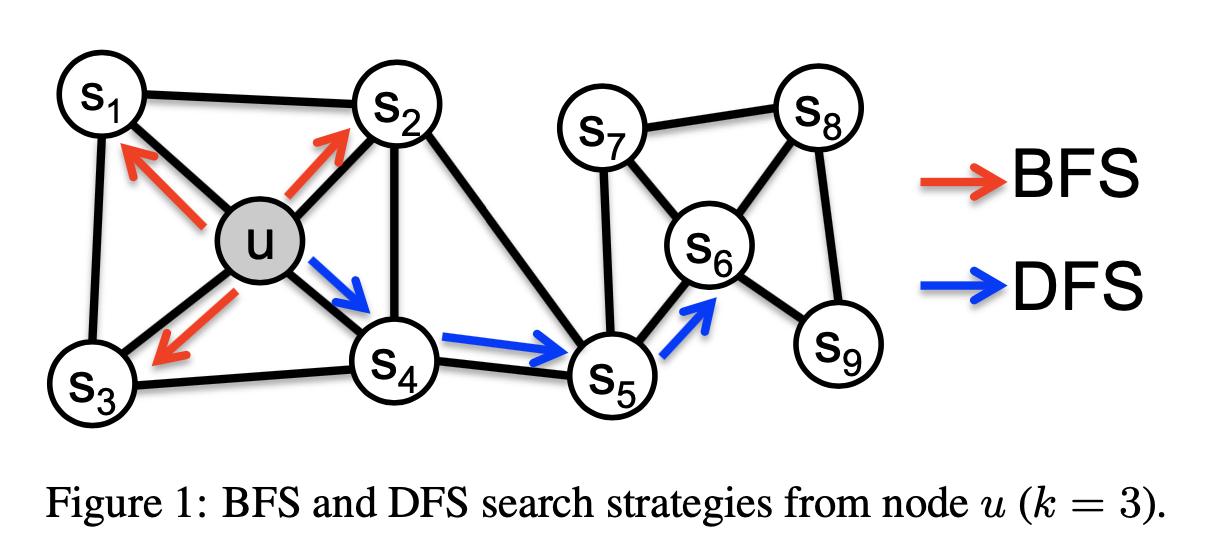
- BFS和DFS的示例
- BFS和DFS的算法

3.2 Cora数据集介绍¶
- Cora数据集由机器学习论文组成。 这些论文分为以下七个类别之一:基于案例、遗传算法、神经网络、概率方法、强化学习、规则学习、理论。这些论文的选择方式是,在最终语料库中,每篇论文引用或被至少一篇其他论文引用。整个语料库中有 2708篇论文。
- 在词干堵塞和去除词尾后(?),只剩下 1433个 唯一的单词。文档频率小于10的所有单词都被删除。
- Cora数据集下载地址:https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz
该数据集由 cora.cites 与 cora.content 两个文件组成。
- .content文件包含以下格式的论文描述:
<paper_id> <word_attributes> <class_label> - 每行(其实就是图的一个节点)的第一个字段是论文的唯一字符串标识,后跟 1433 个字段(取值为二进制值),表示1433个词汇中的每个单词在文章中是存在(由1表示)还是不存在(由0表示)。最后,该行的最后一个字段表示论文的类别标签(7个)。因此该数据的特征应该有 1433 个维度,另外加上第一个字段 idx,最后一个字段 label, 一共有 1433 + 2 个维度。
数据示例:
1061127 0 0 0 0 0 0 0 1 ... 0 1 0 Rule_Learning.cites文件包含语料库的引用关系‘图’。每行(其实就是图的一条边)用以下格式描述一个引用关系:
<被引论文编号> <引论文编号>- 每行包含两个paper id。第一个字段是被引用论文的标识,第二个字段代表引用的论文。引用关系的方向是从右向左。如果一行由“论文1 论文2”表示,则“论文2 引用 论文1”,即链接是“论文2 - >论文1”。可以通过论文之间的链接(引用)关系建立邻接矩阵adj。
数据示例:
35 103482
- .content文件包含以下格式的论文描述:
3.2 Node2Vec流程¶
- 首先,我们设定$G = (V, E)$作为我们的图,其中$V$为图的节点,$E$为图的边。对于任意一个节点$u \in V$,我们模拟一个长度为$l$的随机游走。我们设定$c_i$为随机游走的第$i$个节点,以$c_0=u$作为起始点,其中第$i$个节点$c_i$通过下列概率分布产生:
其中$\pi_{vx}$为是节点$v$和节点$x$的非归一化转移概率,$Z$为归一化常数。
- 最简单的方法是将$\pi_{vx}$直接设为相连边的权重,即$\pi_{vx}=w_{vx}$。这种方式与Deepwalk方法相同。然而这种方法不能充分考虑到图结构的同质性和结构性。因此,通过设定$\pi_{vx}=\alpha_{pq}(t,x)w_{vx}$来调整节点之间的转移概率,其中:
- 以下图所示,其中$t$ 为节点$v$的上一个节点,$d_{t,x}$表示节点$t$与节点$x$的最短距离,例如如果两个节点直接相连,那么$d_{tx}=1$。如果两个节点为相同的节点,$d_{tx}=0$。如果两个节点不相连,则$d_{tx}=2$。参数$p$ 为返回参数,「$p$越小」,节点返回$t$的概率越高,图的遍历越倾向于BFS,「越趋向于表示图的结构性」。参数$q$则被称为进出参数,「$q$越小」,遍历到远处节点的概率越高,图的遍历越倾向于DFS,同时「越趋向于表示图的同质性」。我们可以通过设置$p,q$的值,来权衡graph embedding表达的结果的倾向性。
- 转移概率的设置

- 其中,参数$p, q$分别代表了不同含义:
- 返回概率$p$:如果 $p>\max(q, 1)$ ,那么采样会尽量不往回走,对应上图的情况,就是下一个节点不太可能是上一个访问的节点$t$。如果 $p>\max(q, 1)$,那么采样会更倾向于返回上一个节点,这样就会一直在起始点周围某些节点来回转来转去。
- 出入参数$q$:如果 $q >1$ ,那么游走会倾向于在起始点周围的节点之间跑,可以反映出一个节点的BFS特性。如果 $q<1$ ,那么游走会倾向于往远处跑,反映出DFS特性。
- 特殊的,当 $p=1, q=1$时,游走方式就等同于DeepWalk中的随机游走。
3.4 Node2Vec 代码示例¶
- 安装node2vec包
pip install node2vec
import networkx as nx
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.manifold import TSNE
from node2vec import Node2Vec
# 加载Cora数据集
cora = pd.read_csv('data/cora.content', sep='\t', header=None)
cited_in = pd.read_csv('data/cora.cites', sep='\t', header=None,
names=['target', 'source'])
nodes, features = cora.iloc[:, :-1], cora.iloc[:, -1]
# 定义函数:构造基于Cora数据集的图结构
def create_graph(nodes, features, cited_in):
nodes.index = nodes.index.map(str)
graph = nx.from_pandas_edgelist(cited_in,
source='source',
target='target')
for index, row in nodes.iterrows():
node_id = str(row[0])
features = row.drop(labels=[0])
node_attrs = {f'attr_{i}': float(x) for i, x in enumerate(features)}
if graph.has_node(node_id) == True:
temp = graph.nodes[node_id]
temp.update(node_attrs)
graph.add_nodes_from([(node_id, temp)])
else:
graph.add_nodes_from([(node_id, node_attrs)])
return graph
# 构建图
graph = create_graph(nodes, features, cited_in)
# 定义函数:创建基于Cora数据集的嵌入
def create_embeddings(graph):
# 初始化node2vec实例,指定相关超参数
n2v = Node2Vec(graph, dimensions=64, walk_length=4,
num_walks=10, p=1, q=1, weight_key='attr_weight')
# 基于指定参数训练得到嵌入向量表达式
model = n2v.fit(window=10, min_count=1, batch_words=4)
# 获得所有图中节点的嵌入向量
embeddings = pd.DataFrame(model.wv.vectors)
ids = list(map(str, model.wv.index_to_key))
# 将原有的特征和id与新获取到的嵌入向量按行合并
lookup_table = nodes.set_index(0).join(embeddings.set_index(embeddings.index))
return np.array(lookup_table.dropna().iloc[:, -64:]), np.array(list(range(1, lookup_table.shape[0] + 1)))
# 创建嵌入向量
cora_embeddings, cora_labels = create_embeddings(graph)
from sklearn import svm, model_selection, metrics
# 使用支持向量机作为示范的分类器
svm_model = svm.SVC(kernel='rbf', C=1, gamma=0.01)
# 进行交叉验证和分类训练
scores = model_selection.cross_val_score(
svm_model, cora_embeddings, cora_labels, cv=5)
print(scores.mean())
# 定义函数:可视化Nodes2Vec的结果
def visualize_results(embeddings, labels):
# 使用t-SNE对数据进行降维并绘图
tsne = TSNE(n_components=2, verbose=1, perplexity=40, n_iter=300)
tsne_results = tsne.fit_transform(embeddings)
plt.figure(figsize=(10, 5))
plt.scatter(tsne_results[:,0], tsne_results[:,1], c=labels)
plt.colorbar()
plt.show()
# 可视化结果
visualize_results(cora_embeddings, cora_labels)
4. GNN简介¶
4.1 GNN简介¶
一句话概括图神经网络(Graphic Nuaral Network,GNN):将一个数据(一个图)输入到网络(GNN)中,会得到一个输出数据(同样是图),输出的图和输入的图相比,顶点、边、以及全局信息会发生一些改变。(注意,顶点之间的连接情况不会变)
GNN历史
- 1997年首先在图上用神经网络
- GNN在2005年被首次提出
- 早期是研究RecGNN,通过迭代地传播邻居信息直到收敛,得到node representation
- CNN火了之后开始有ConvGNN,分为谱域卷积(spectral-based approaches)和空域卷积(spatial-based approaches)
一些参考资料
- 图神经网络的基本原理 https://blog.csdn.net/Cyril_KI/article/details/122058881
- 【GNN入门】综述篇 https://zhuanlan.zhihu.com/p/430518493
- A Gentle Introduction to Graph Neural Networks https://distill.pub/2021/gnn-intro/
- 李沐的B站讲解:https://www.bilibili.com/video/BV1iT4y1d7zP/
4.2 一篇关于GNN的文献回顾¶
- Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and P. S. Yu, "A Comprehensive Survey on Graph Neural Networks," in IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 1, pp. 4-24, Jan. 2021, doi: 10.1109/TNNLS.2020.2978386.
对这篇文章的解读:https://zhuanlan.zhihu.com/p/538914712
- 第1节Introduction简要介绍了本文内容,总结了本文贡献。
- 第2节中简单介绍了GNN的发展历史,给出了GNN中的一些定义(需要区分特征向量和状态向量),然后对GNN和图嵌入进行了区分和联系。
- 第3节中给出了一个GNN的分类原则,将GNN分为四类:recurrent GNN (RecGNN,循环GNN)、convolutional GNN(ConvGNN,卷积GNN)、graph autoencoder(GAE,图自编码器)和spatial-temporal GNN (STGNN,时空GNN)。第3节还从Node Level、Edge Level和Graph Level三个方面来介绍了GNN的输出形式,同时探讨了GNN的(半)监督学习和无监督学习框架。
- 第4节介绍了RecGNN的相关知识。在之前的一篇文章中对GNN的原始论文进行了解读,实际上这就是一种RecGNN。RecGNN的核心是消息传递机制:通过不断交换邻域信息来更新节点状态,直到达到稳定均衡(相互连接的节点间交换信息,GNN核心)。在本节中作者介绍了门控GNN(Gated GNN,GGNN)和随机稳态嵌入(SSE)两种RecGNN。
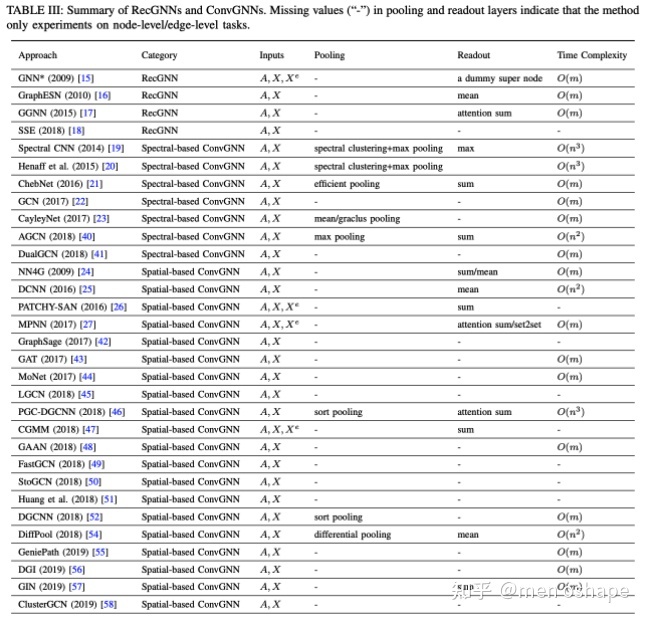
- 第5节介绍了ConvGNN的相关知识。之前的一篇文章里实际上已经对ConvGNN的大致原理进行了讲解。与RecGNN使用相同的图循环层(Grec)来更新节点的表示不同的是,ConvGNN使用不同的图卷积层(Gconv)来更新节点表示。ConvGNN分为基于频域的ConvGNN和基于空间域的ConvGNN。基于频域的ConvGNN借助图的拉普拉斯矩阵的特征值和特征向量来研究图的卷积,而基于空间域的ConvGNN则是基于节点的空间关系来定义图卷积。基于频域的ConvGNN主要介绍了Spectral CNN、ChebNet、CayleyNet和AGCN等,基于空间域的ConvGNN主要介绍了NN4G、DCNN、PGC-DGCNN。此外,本节还探讨了GNN中的Pooling,常见的Pooling操作有:sum、max以及mean,此外还介绍了SortPooling和DiffPool等一些变种。
- 第6节介绍了GAE的相关知识。GAE是一种将节点映射到潜在特征空间并从其潜在表示中解码图形信息的深层神经网络。简单来说,需要先学习节点的状态向量,然后再从其中解码出图信息。因此,GAE一般用于学习网络嵌入表示或者来生成新的图。用于学习网络嵌入的GAE,作者介绍了DNGR、SDNE和VGAE。用于图生成的GAE,作者介绍了DeepGMG和GraphRNN。
- 第7节介绍了STGNN的相关知识。在许多真实世界的应用程序中,图在图结构和图输入方面都是动态的。STGNN在图的动态捕捉中占有重要的地位,这类方法的目标是在假定连接节点之间相互依赖的情况下,对动态节点输入进行建模。STGNN同时捕获图的空间和时间依赖性,其任务可以是预测未来的节点值或标签,也可以是预测时空图标签。 STGNN有两个方向:基于RNN的方法和基于CNN的方法。基于RNN的STGNN,作者介绍了GCRN和DCRNN。基于CNN的STGNN,作者介绍了CGCN和ST-GCN。
- 第8节介绍了GNN的一些应用。关于GNN,有两个比较流行的框架:PyTorch Geometric和DGL。GNN在实际生活中的应用主要包括:CV领域(场景图生成、点云分类和动作识别)、NLP领域(文本分类和机器翻译)、交通领域(预测交通网络中的交通速度、交通量或道路密度,出租车需求预测)、推荐系统、化学领域(分子指纹图谱、预测分子性质、推断蛋白质结构以及合成化合物)、其他领域(如程序验证、程序推理、社会影响预测、对抗攻击预防、脑网络、事件检测、组合优化等)。
- 第9节作者给出了GNN未来可能的4个研究方向:深入学习图表数据是否是一个好的策略?如何权衡算法的可扩展性和图的完整性?异质图如何有效地处理?动态图中如何进行有效卷积?
- 第10节为总结。
- GNN的种类
4.3 GNN的应用场景¶
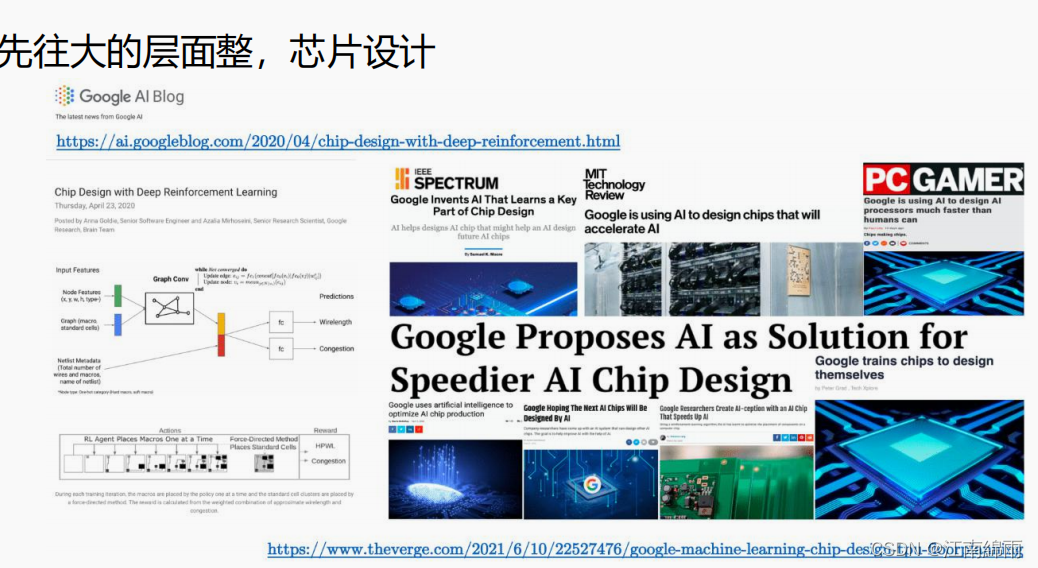


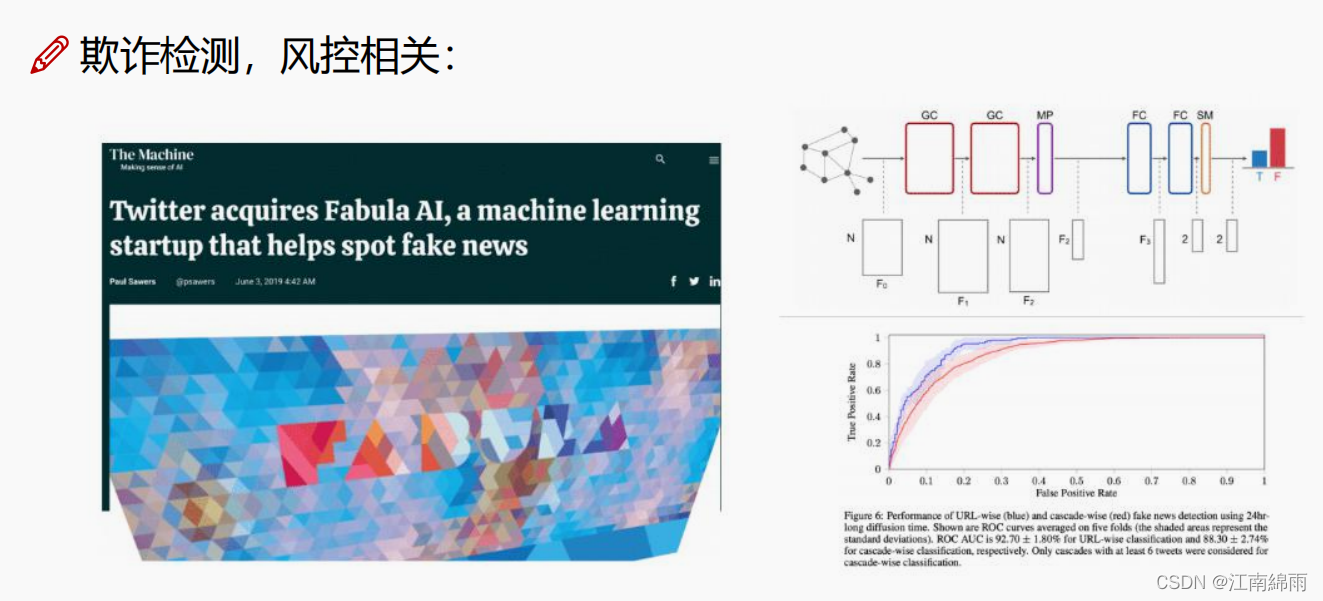
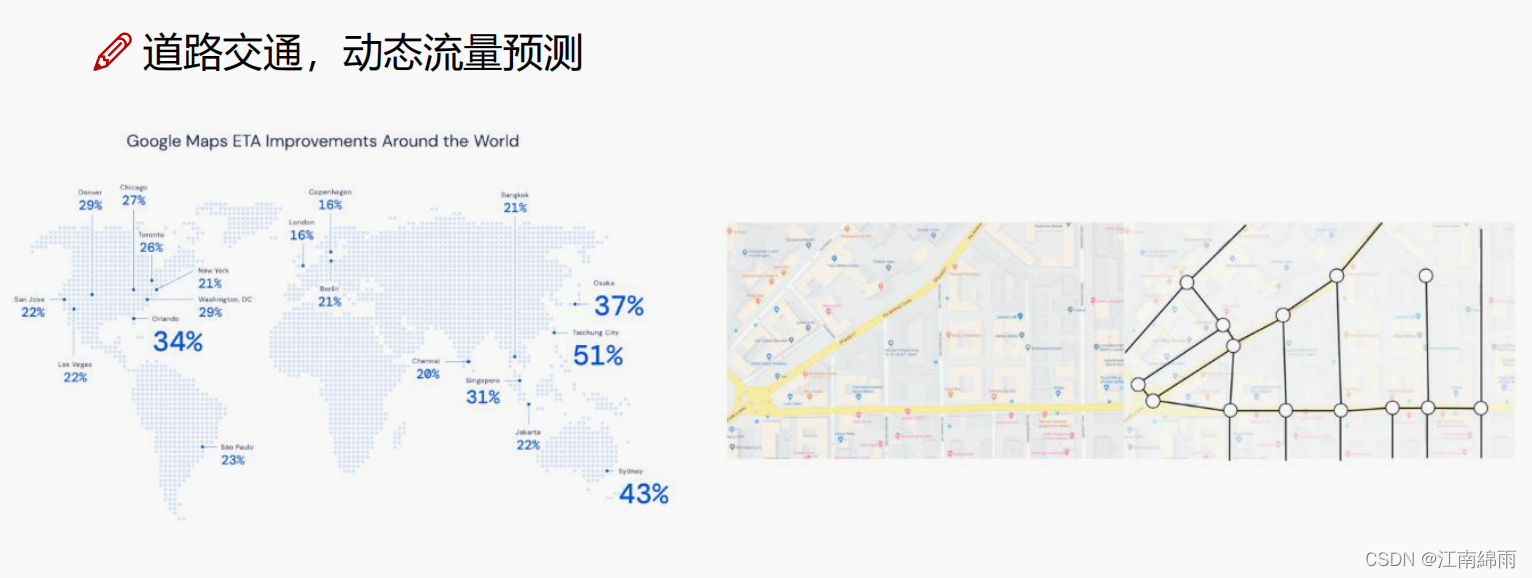
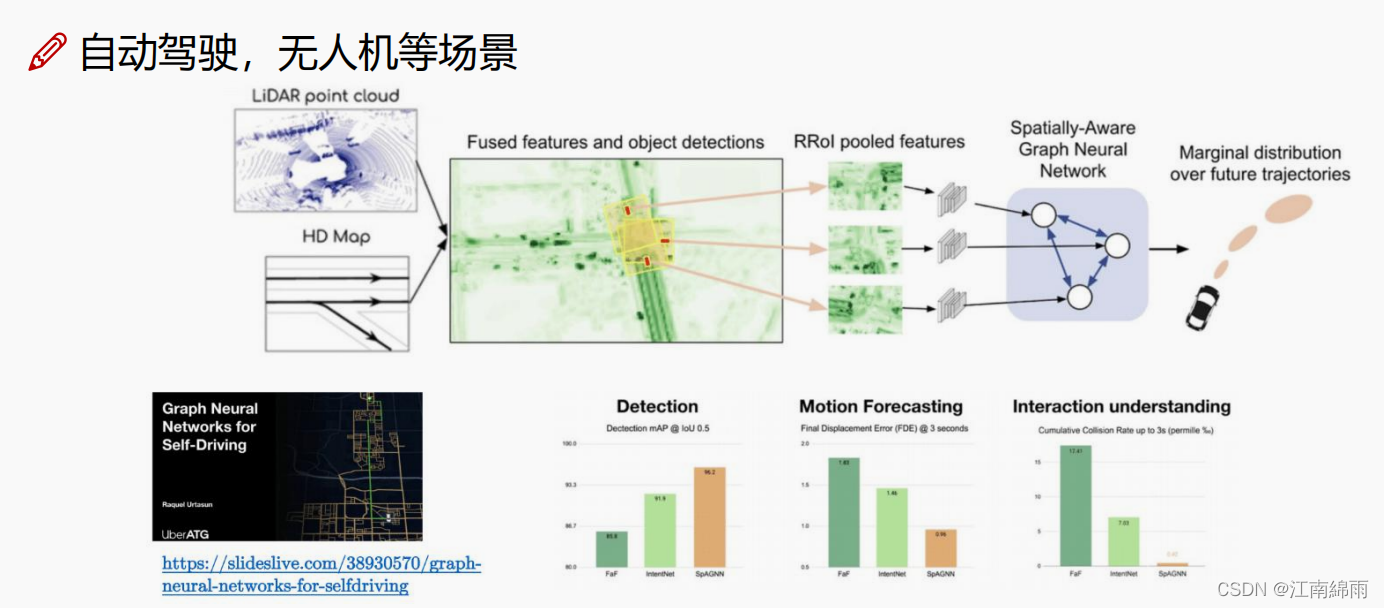
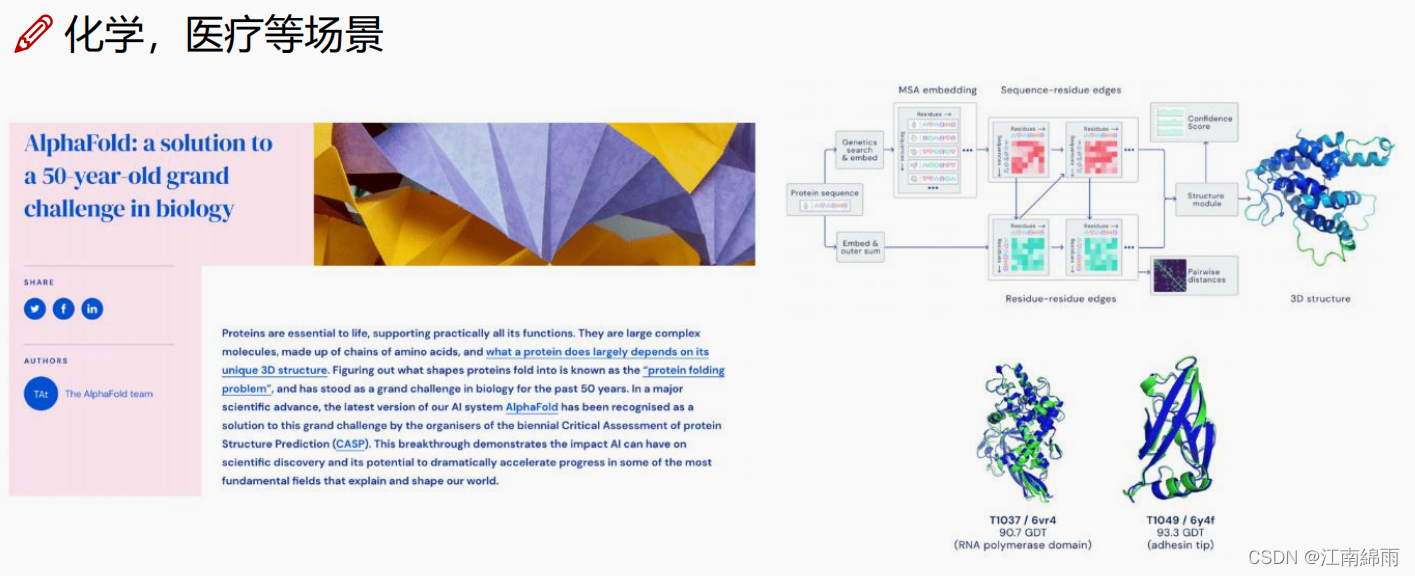
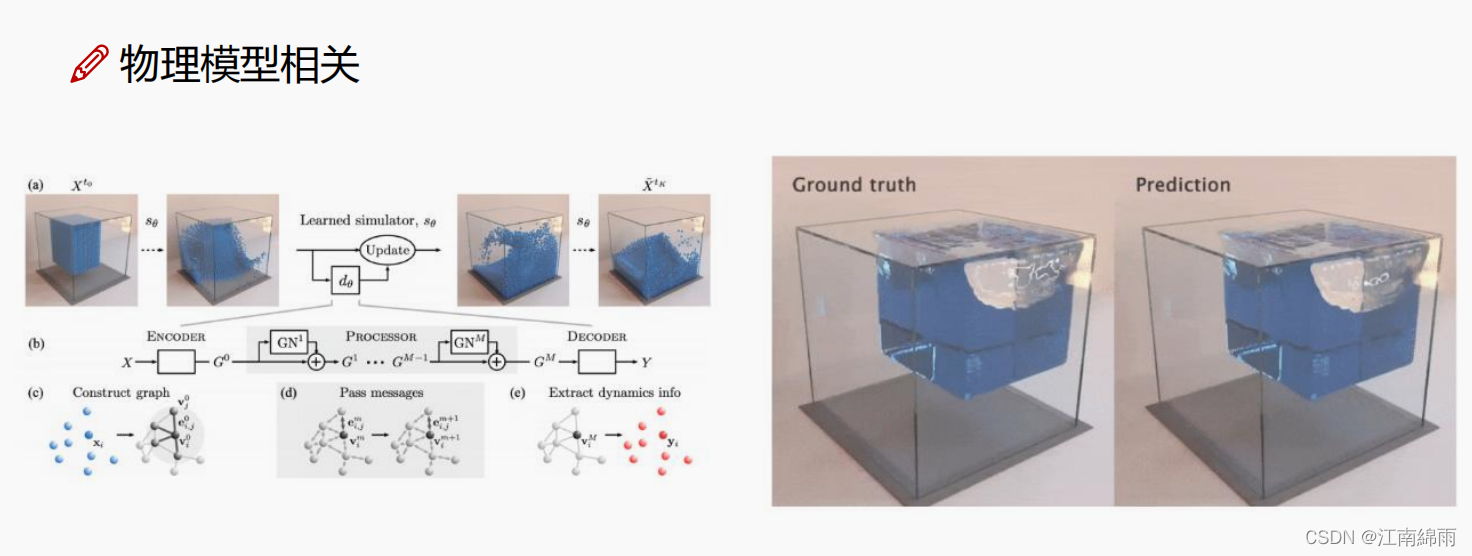
4.4 GNN的原理¶
内容参考:https://blog.csdn.net/weixin_43702653/article/details/123779738?spm=1001.2014.3001.5502
4.4.1 GNN与邻接矩阵¶
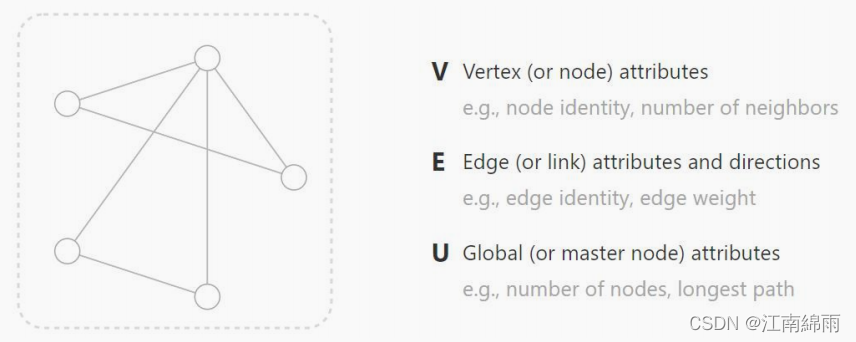
- GNN全称----图神经网络,它是一种直接作用于图结构上的神经网络。我们可以把图中的每一个节点 $V$ 当作个体对象,而每一条边 $E$ 当作个体与个体间的某种联系,所有节点组成的关系网就是最后的图 $U$。
- 这里的$V,E,U$都可以编码成一个特征向量,所以实际上GNN还是做的是提取特征的工作而已。GNN的一个典型应用是节点分类,我们希望利用GNN提取出每个节点 $V$ 的特征向量,来预测每个节点的标签。同样的,也可以通过节点与节点间的特征,来预测出对应边 $E$ 的标签。当然,也可以利用所以节点提取出的特征,来预测整个图 $V$ 的标签。
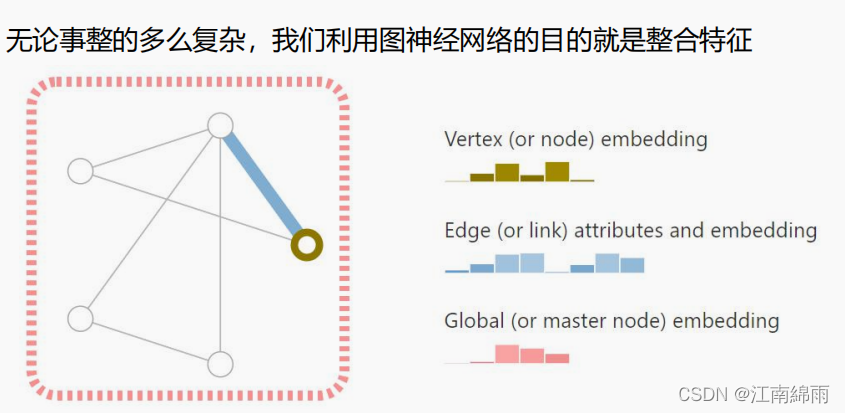
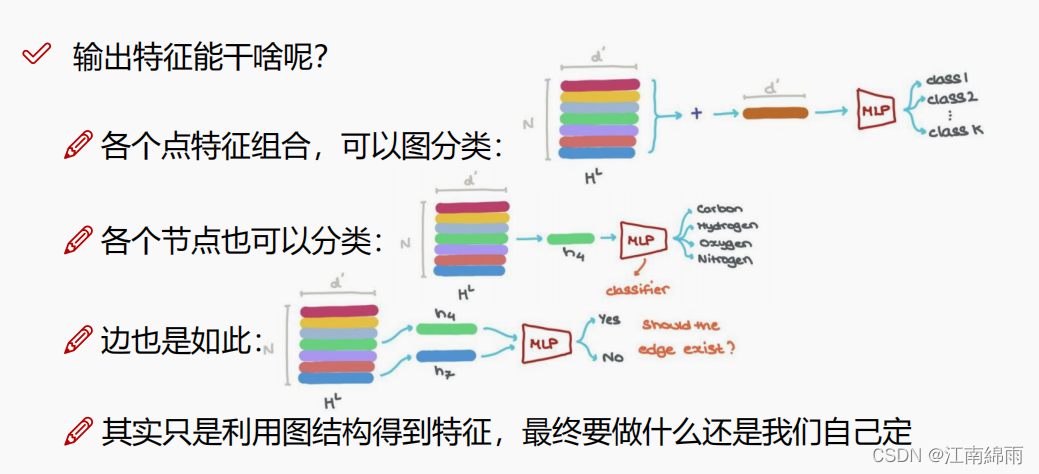
4.4.2 聚合操作¶
- GNN的输入一般是每个节点的起始特征向量和表示节点间关系的邻接矩阵,有了这两个输入信息,接下来就是聚合操作了。所谓的聚合,其实就是将周边与节点 $V_i$ 有关联的节点${V_a,V_b,...}$加权到$V_i$上,当作一次特征更新。同理,对图中的每个节点进行聚合操作,更新所有图节点的特征。
- 聚合操作的方式多种多样,可根据任务的不同自由选择,如下图所示:
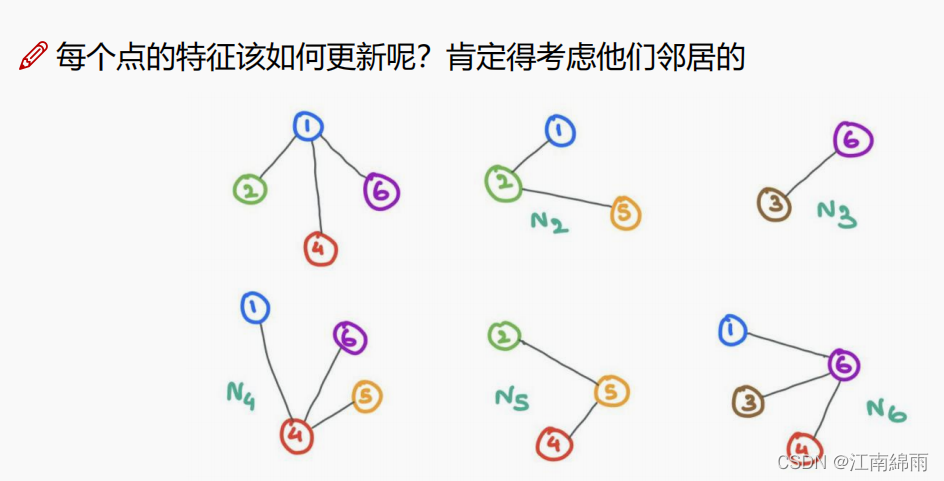

4.4.3 多层迭代¶
- CNN,RNN都可以有多个层,那么GNN也当然可以。一次图节点聚合操作与 $w$ 加权,可以理解为一层,后面再重复进行聚合、加权,就是多层迭代了。一般GNN只要3~5层即可,所以训练GNN对算力要求很低。如下图所示:

5. GCN简介(2017年)¶
5.1 GCN论文¶
Kipf, Welling, 2017, SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS, ICLR 2017
b站UP主 望舒同学 讲解GCN:https://www.bilibili.com/video/BV1z14y1A7JX/
5.2 GCN的基本原理¶
原文链接:https://blog.csdn.net/weixin_43702653/article/details/123850998
此卷积非彼卷积,完全不是一码事,只是说GCN也可以做多层罢了。。。如下图:
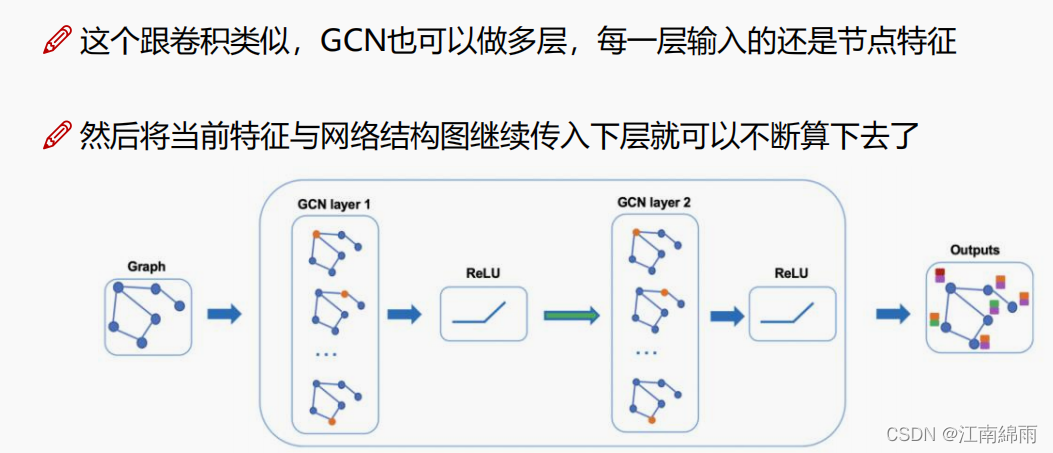
- GCN的核心计算公式:
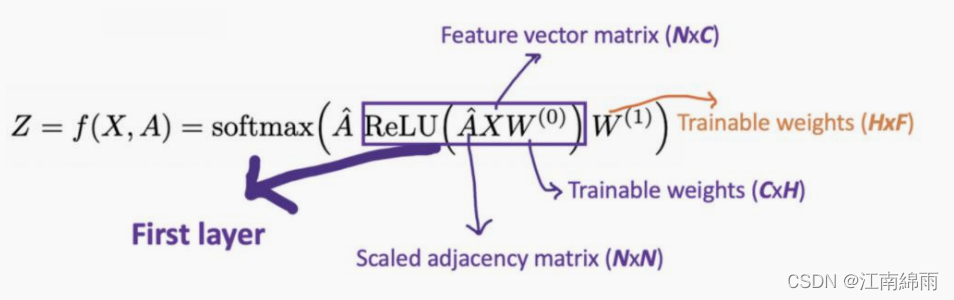
5.2.1 Step1: 求图模型的邻接矩阵和度矩阵¶
- 对于传统的GNN,一个图网络需要节点特征矩阵和邻接矩阵的输入,这样才能进行节点的聚合操作。但是GCN中还需要引入一个度矩阵,这个矩阵用来表示一个节点和多少个节点相关联,对于后面的步骤有巨大的作用,如图所示:
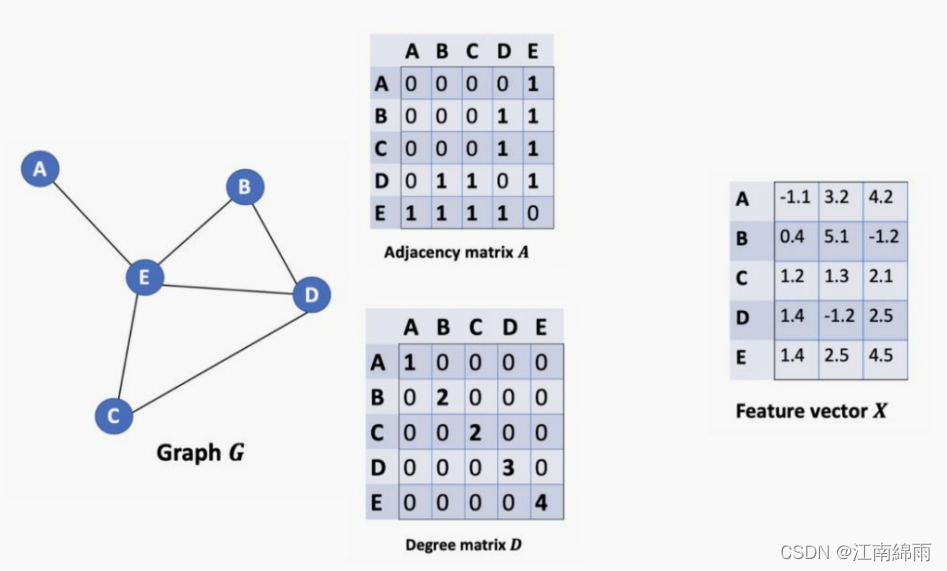
5.2.2 Step2:进行特征计算¶
- 求得矩阵$A,D,X$后,进行特征的计算,来聚合邻居节点的信息。GCN中的聚合方式和传统GNN中的方式有较大差异,这里分解为几个细节点:
① 邻接矩阵的改变
- 邻接矩阵 $A$ 没有考虑自身的加权,所以GCN中的邻接矩阵实际上等于 $A$ +单位对角矩阵 $I$。
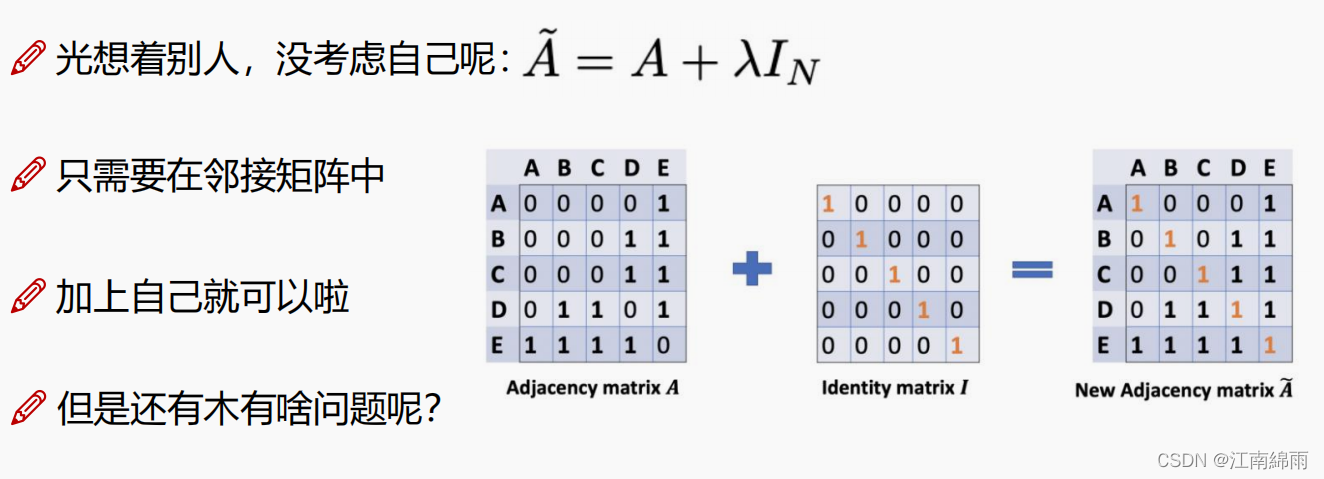
② 度矩阵的改变
首先对度矩阵的行和列进行了归一化(具体格式看下图),为什么这么做呢?行归一化系数代表着节点自身的一个变化程度,关联的节点越少,系数越大,越容易随波主流,更易受别人影响。而列归一化系数,代表关联节点对当前节点的影响程度,关系网越复杂的节点,它对其他节点的作用就越小,比如我认识一个亿万富翁,但富翁认识很多人,我们也就是一面之缘,那么能说因为我和他认识,我就是个百万富翁了嘛,显然有点草率了。通过行和列归一化系数,相互制衡。
同时,归一化的系数还开了根号,就是因为考虑到归一化后的行和列系数都加权给了节点特征,均衡一点。
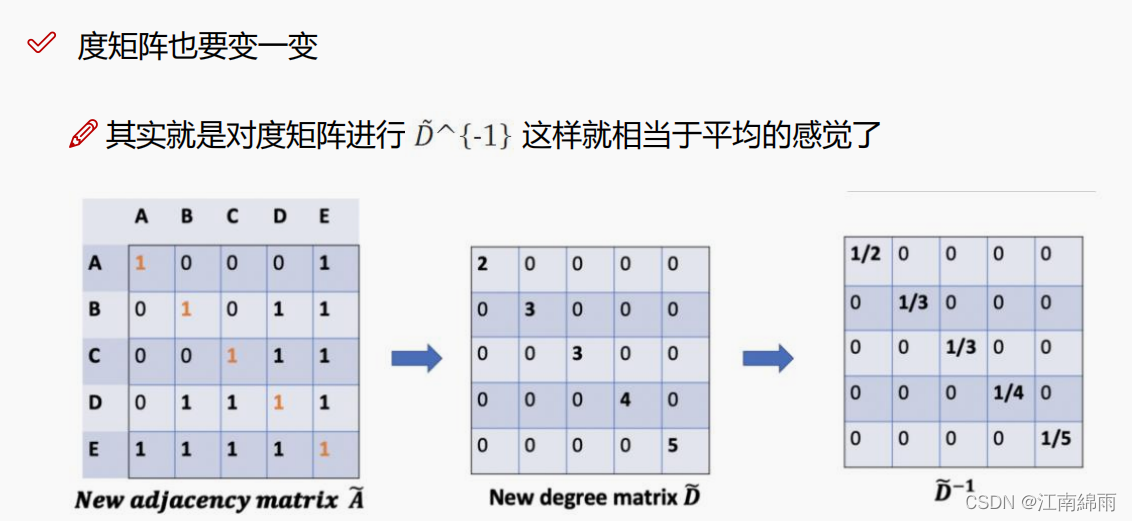
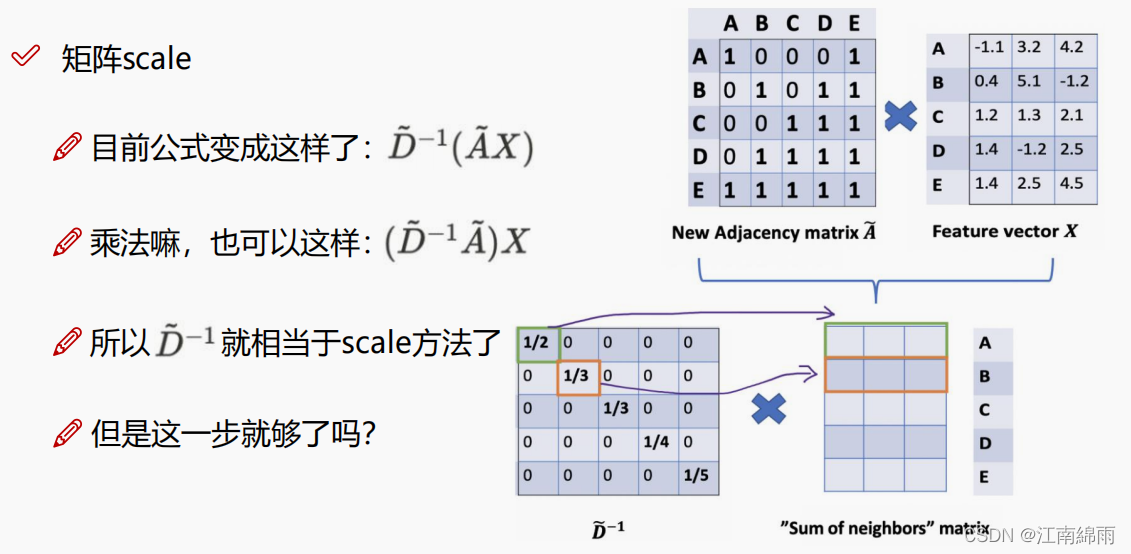
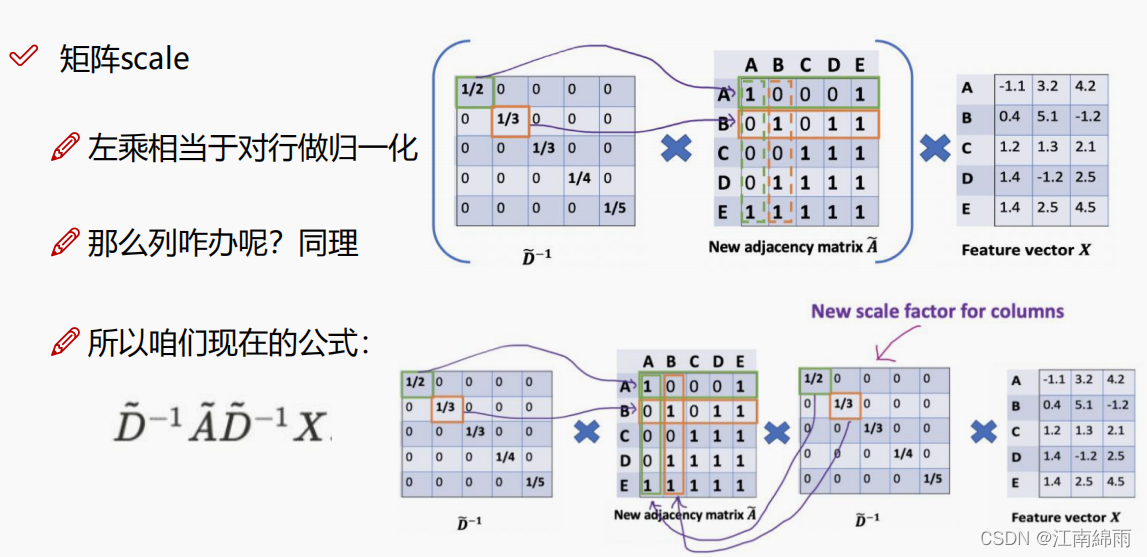


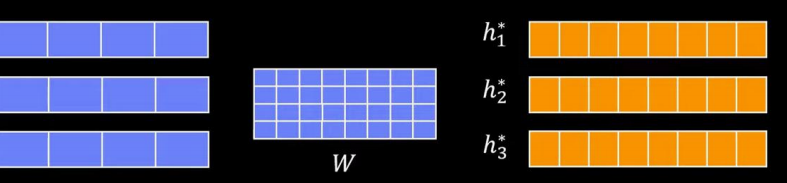
③ Attention机制
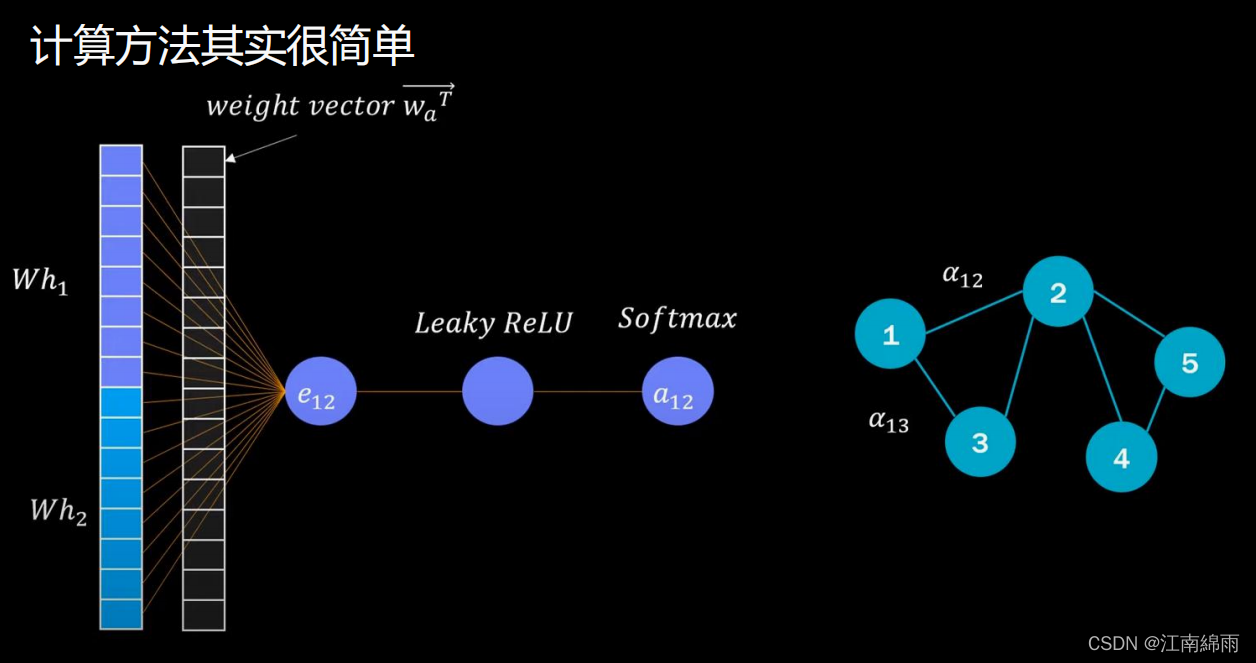
- 在部分GCN中,还会引入注意力机制,根据关联节点的重要性来分配权重,最后乘到邻接矩阵上。传统计算权重的方法有两种,第一种方法,两节点特征向量直接相乘,关联节点都算完后,经过softmax算出权重值。还有第二种方法,就是将本节点和关联节点拼接成一个特征向量后,传入FC中,最后经过softmax算出权重值。如图所示:

5.2.4 Step 4:层数的迭代¶
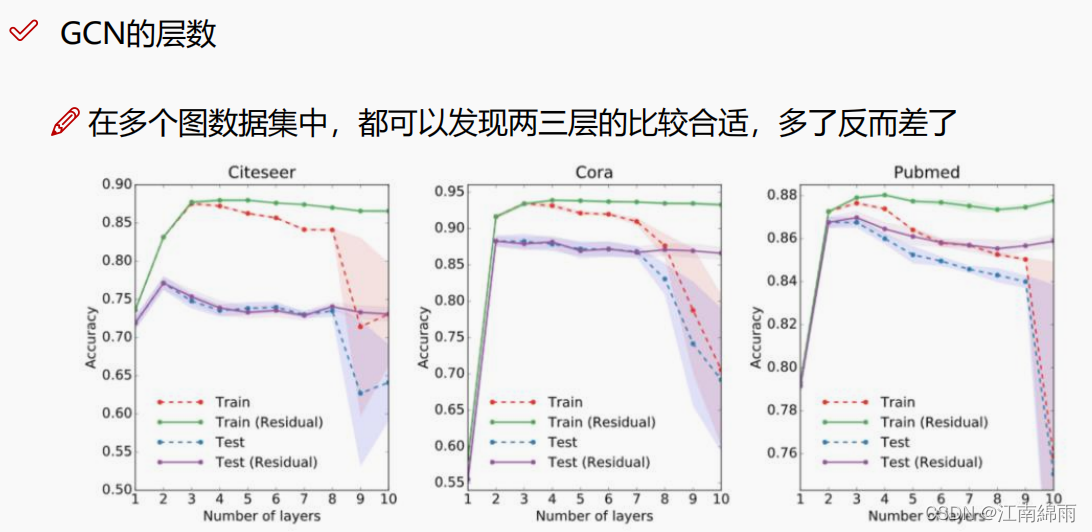
接下来重复step1~3,每重复一次算一层,GCN正常只需要3–5层即可,这里就和CNN、RNN很不一样。因为节点每更新一次,感受野就变大一些,如果网络太深,那么每个节点就会受无关节点的影响,效果反而下降。
正如六度分割空间理论——“只需6个人,你就可以认识全世界”,见下图所示: